Pan Tilt Roll Rotation Matrix

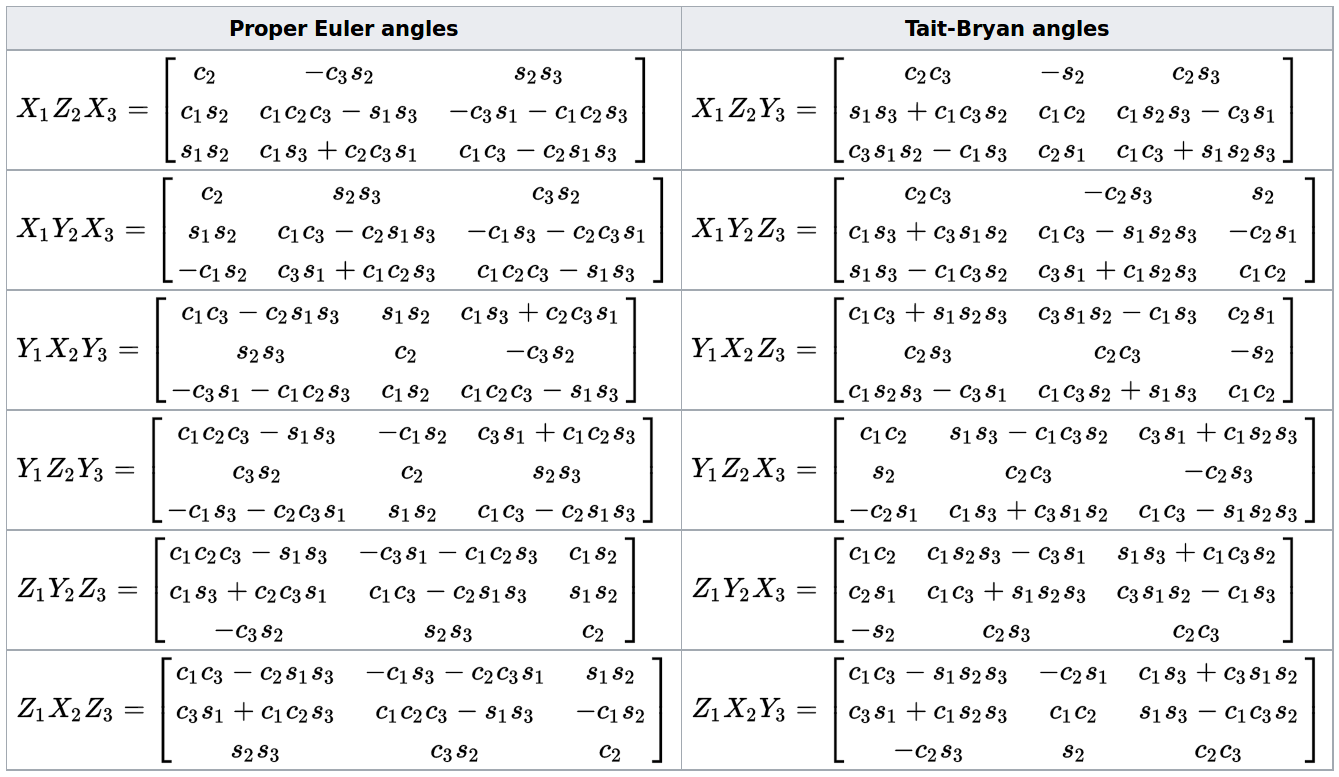
Given 3 euler angles the rotation matrix is calculated as follows.

Pan tilt roll rotation matrix. Given a 3 3 rotation matrix. Note on angle ranges. Double roll math atan side z math sqrt side x side x side y side y. Unit vector axis and angle convention.

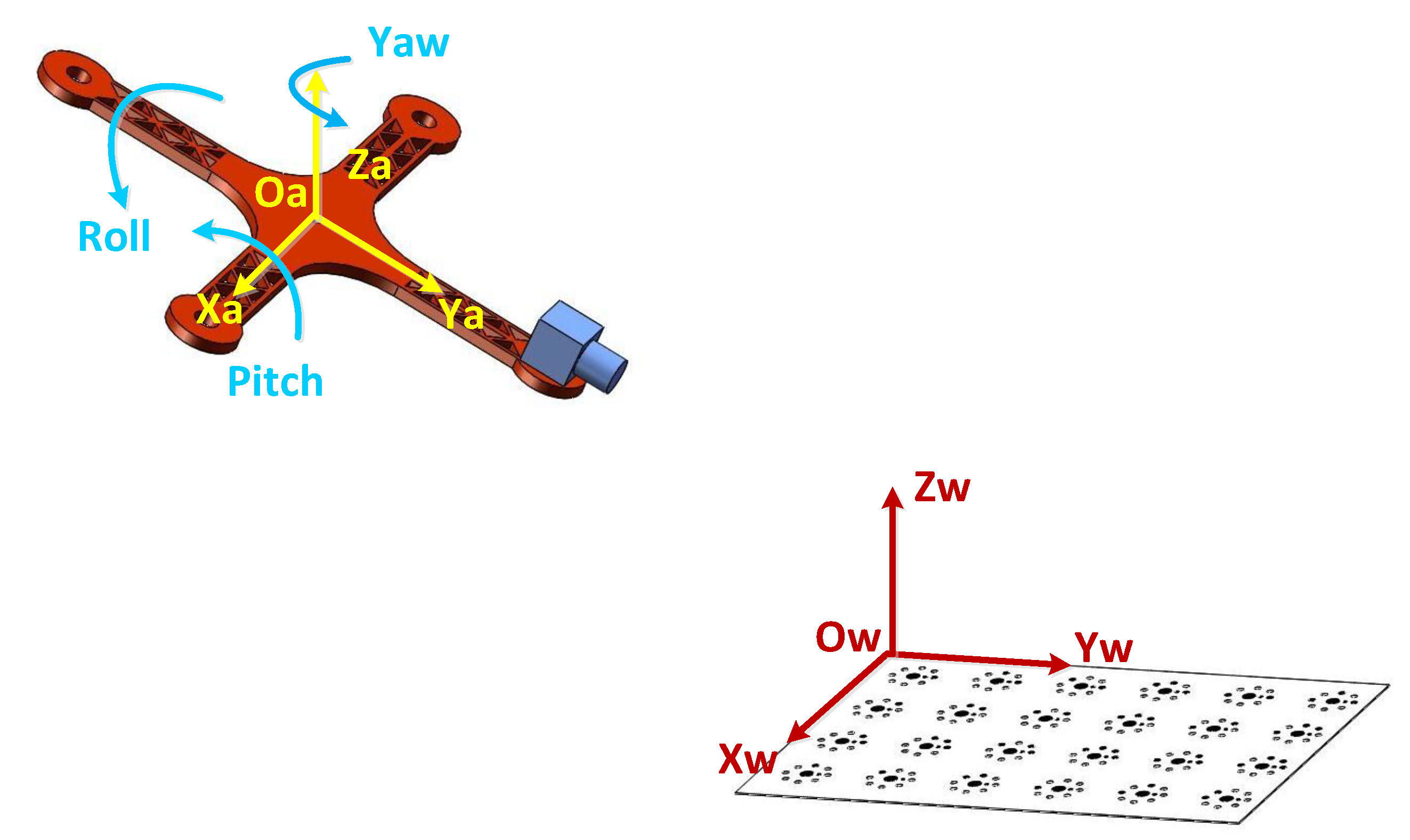
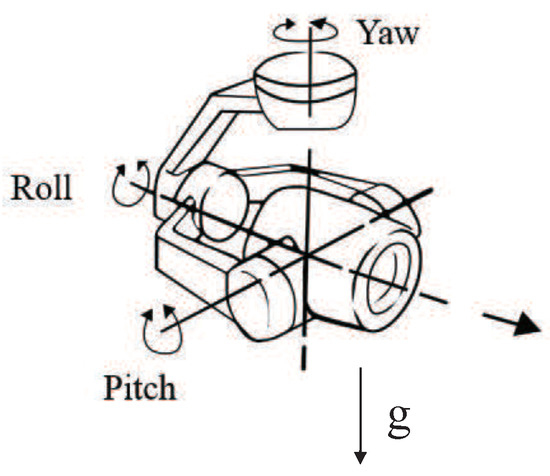
An entity can be rotated by changing these values. A roll movement indicates a rotation about the front axis. Use the yaw pitch and roll values to generate a rotation matrix equation 9 use the rotation matrix to rotate all the points that make up the aircraft equation 6a 6b and 6c now the aircraft is rotated where we want it so far so good. X r y r image coordinates after roll movement.

Here atan2 is the same arc tangent function with quadrant checking you typically find in c or matlab. In this report instead of a single focal length and the aspect ratio another equivalent representation of two focal lengths f x and f y is used. T x ty z translation matrix. 0 pan 360 tilt is the angle of rotation around x from down down up corresponds to zenith.

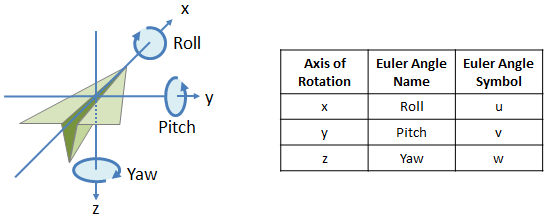
Angles are given in degrees 0 to 360 and counted counter clockwise. Entity pan can also serve as angle vector. In 2d a rotation just has an angle in 3d specifying a rotation is more complex basic rotation about origin. A pan yaw movement indicates rotation about the top axis.

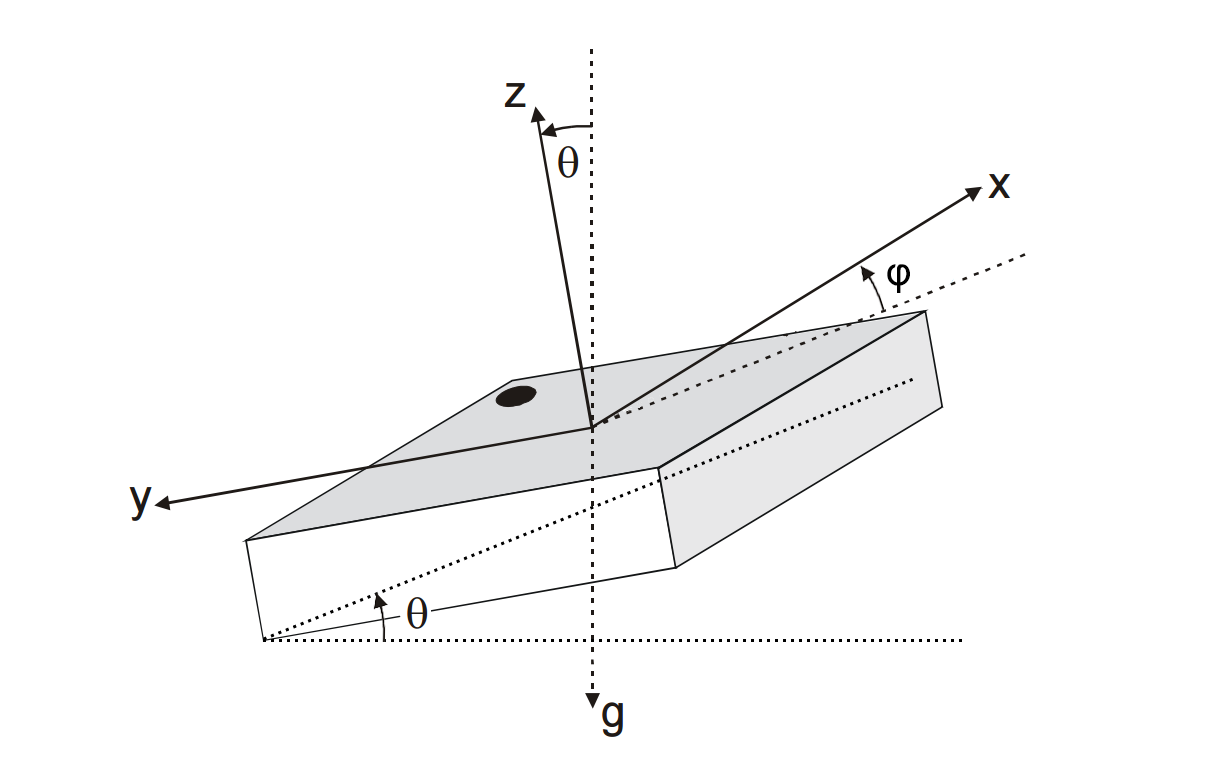
This allows the camera to point left right and in between. 0 tilt 180 roll is the angle of rotation around y clockwise side to side depends on horizon line 0 roll 360. Decomposing a rotation matrix. Pan tilt roll the euler angles that describe rotations about the z y and x axis in degrees 0 360.

Pan is the angle of rotation around z from north left right corresponds to azimuth. Each rotation matrix is a simple extension of the 2d rotation matrix for example the yaw matrix essentially performs a 2d rotation with respect to the and coordinates while leaving the coordinate unchanged. The 3 euler angles are. The range of the tilt movement is very important as it controls your ability to capture shots above or below the drone.

Spatial rotations in three dimensions can be parametrized using both euler angles and unit quaternions this article explains how to convert between the two representations. For rotations in three dimensions the so called euler. Positive rotation is ccw when vector is pointing at you many ways to specify rotation indirectly through frame transformations directly through euler angles. If the camera rotates by a rotation matrix r and.

Thus the third row and third column of look like part of the identity matrix while the upper right portion of looks like the 2d rotation matrix.